1-8 コード生成３

最終回では、コード生成に関係する話題で、これまで取り上げられなかったものをひろって解説する。

ループ

while 文のコンパイルは if 文のコンパイルとそれほど違いはなく、分岐がわずかに複雑になるだけである。

while (i < n) {
    i = i + 1;
}
return i;

このプログラムは例えば次のようにコンパイルすればよい。

L1:
    式 i < n のコンパイル結果 (%edx に結果が保存される)
    cmpl $0, %edx
    je L2
    文 { i = i + 1; } のコンパイル結果
    jmp L1
L2:
    文 return i のコンパイル結果

L1, L2 はラベルである。while 文の制御構造をそのまま分岐命令に置きかえていることがわかるだろう。

if 文の場合、分岐命令への置きかえ方はほとんど一通りであるが、while 文の場合はいくつかの置きかえ方が考えられる。上の例は、while 文の制御構造そのままで直観的だが、ループを回る度に分岐命令 jmp と je (ループを抜けるとき以外は分岐しない)を2つ実行しなければならない。一般に、分岐命令は演算命令に比べて遅いので、while 文を次のようにコンパイルするようにすれば、より高速な実行が期待できる。

    jmp L2
L1:
    文 { i = i + 1; } のコンパイル結果
L2:
    式 i < n のコンパイル結果 (%edx に結果が保存される)
    cmpl $0, %edx
    jne L1
    文 return i のコンパイル結果

分岐命令 jne は jump on not equal の意味で、0 (zero) と %edx のが等しくなければ L1 に分岐する。

上のようにコンパイルすると、一回のループごとに分岐命令 jne を一回しか実行しなくてよい。その分、ループの一回目に L2 へ分岐するための無条件分岐命令 jmp を実行しなければならないが、 これはループ全体につき 1 回だけなので、ループの回数が増えれば増えるほど影響は小さくなる。

while 文がコンパイルできれば、for 文のコンパイルも容易である。

for (i = 0; i < n; i = i + 1) {
    j = j + 1;
}
return i;

このプログラムは例えば次のようにコンパイルすればよい。

    文 i = 0; のコンパイル結果
L1:
    式 i < n のコンパイル結果 (%edx に結果が保存される)
    cmpl $0, %edx
    je L2
    文 { j = j + 1; } のコンパイル結果
    文 i = i + 1 のコンパイル結果
    jmp L1
L2:
    文 return i のコンパイル結果

基本は while 文のコンパイルと同様である。また while 文でしたような工夫をすれば、for 文もループ一回あたりの分岐命令の数を減らすことができる。

ループの最適化

ループ内不変式のくくり出し

for (i = 0; i < n; i = i + 1)
    s = s + x[i + k + 1];

ループ中で i + k + 1 を計算しているが、このうち k の値はループの間中、変化しない。従って k + 1 の値も変化しないので、あらかじめループの外で k + 1 を計算しておいた方がよい。

temp = k + 1;
for (i = 0; i < n; i = i + 1)
    s = s + x[i + temp];

このように k + 1 の値をあらかじめ計算して、変数 temp に代入し、ループ中では temp を参照するようにすれば、ループ一回ごとに加算命令をひとつ節約できる。temp の値を変数(メモリ)に退避せずに、適当なレジスタ上においておけば、より高速実行できる。

注：ここでは見やすくするために、ソースコード・レベルで不変式をくくりだしたが、実際のコンパイルでは、ソースコード・レベルの変換はおこなわず、上記のプログラムに対応する機械語命令を直接出力する。

Loop unrolling

for (i = 0; i < 3; i = i + 1)
    foo(i);

この場合、ループの回数は3と決まっているので、

foo(0);
foo(1);
foo(2);
i = 3;

と3回分のループを並べて(unrolling)しまえばよい。

ループの回数があらかじめわかっていなくても、部分的に unrolling することができる。

for (i = 0; i < n; i = i + 1)
    foo(i);

これを3回分 unrolling すると、

for (i = 0; i < n - 2; i = i + 3) {
    foo(i);
    foo(i + 1);
    foo(i + 2);
}

if (i < n)
    foo(i);

if (i < n - 1)
   foo(i + 1);

i = n;

ループの内部では3回分まとめて実行するので、分岐命令の数は約 1/3 に減る。ただしループ終了後、3 の端数回分のループを実行しなければならない。

Tail recursion

C 言語などの手続型の言語ではあまり使われないが、Lisp などの関数型の言語では、繰り返し構造を表現するのに、関数の再帰呼出しがよく使われる。

int f(int i, int j) {
    if (i == 0)
        return j;
    else
        return f(i - 1, j + i);
}

関数呼出しは、分岐命令よりもさらに時間のかかる処理なので、上のような関数は、 tail recursion という技法を使ってループ構造に変換してコンパイルされる。

int f(int i, int j) {
    for(;;)
        if (i == 0)
            return j;
        else {
            int i2 = i - 1;
            int j2 = j + i);
            i = i2;
            j = j2;
        }
}

元の関数 f() 中の再帰呼出し f(i - 1, j + i) が終了したら、呼んだ側の関数 f() も終了するので、再帰呼出しのために新たにスタック・フレームを用意する必要 はない。

レジスタ割り当て

式の途中結果をメモリに退避せずに、空いているレジスタがあるときには、そのレジスタに退避するためのアルゴリズムを以下に示す。

例えば a = a + b - 3 をコンパイルするとしよう。

まず無限個のレジスタ (r1-rN) があると仮定して、プログラムをコンパイルする。レジスタ数は無限個なので、式の途中結果は全てレジスタに退避する。

movl 変数 a, r1
movl 変数 b, r2
addl r1, r2
movl $3, r3
subl r3, r2
movl r2, 変数 a

何か新しい値を計算する度に、新しいレジスタを使っていることに注意。

次に同時に使われないレジスタは同じレジスタを使うようにして、全体として使用されるレジスタの個数を減らす。例えば、r1 は addl 実行後は使われないので、r3 を r1 で置きかえることができる。

このようなレジスタの置きかえを計算する方法として register coloring (彩色) が知られている。

(1) まずそれぞれのレジスタの liveness を解析する。liveness とは、プログラムのどの部分からどの部分の間で、そのレジスタが使われているか、である。上の例では、レジスタ r1 の liveness は最初の 3 行である。

(2) 解析結果をもとに、プログラムの各ステップで live なレジスタの集合を計算する。例えば 4 行目の実行時には r2, r3 が live である。

(3) 干渉グラフを作る。干渉グラフのノードは各レジスタで、エッジ (s, t) はノード s と t が同時に live であることを表わす。

(4) 実際に使用可能なレジスタが K 個であるとして、K 個のレジスタを干渉グラフのノードに割り振る。このとき、エッジ (s, t) が存在するときには、s と t に同じレジスタを割り振ってはいけない。

K 個のレジスタの割り振りは問題は、地図を K 色で塗り分ける問題と等価なので、register coloring と呼ばれる。地図の塗りわけ問題の場合、ノードは国、エッジは隣接している国の関係を表わす。

この問題は NP 完全であるが、実用的には次のような近似アルゴリズムが知られている。

1. 干渉グラフ中から、エッジが K - 1 本以下だるノードを選び、グラフから取り除く。

2. グラフが空になるか、それ以上ノードを取り除けなくなるまで 1 を繰り返す。

3. グラフが空になった場合、塗りわけは可能である。 1 の繰り返しを逆にたどり、ノードとエッジをグラフに付加していく。 ノードを付加するたびに、エッジで結ばれている隣接ノードとは異る色を、そのノードに割り当てていく。

4. グラフが空にならない場合、そのままでは塗りわけられない。 適当なノードを選びグラフから除去して、2 を続ける。 取り除いたノードが表わすレジスタの値はメモリに退避することにする。

どのノードを選んで除去するかによって、最終的に生成される機械語命令の性能は変化する。 このアルゴリズムを実装する際には、レジスタ内の値の利用頻度などを勘案して、適切なノードを選ぶようにしなければならない。

(5) 割り振ったレジスタに従って、実際の機械語命令を生成する。

関数引数の渡し方

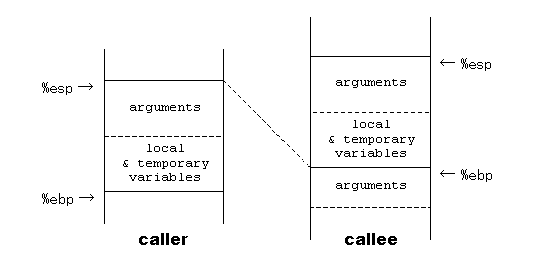
C 言語の場合、関数引数は関数の呼出し側のスタック・フレームの最上部に積まれる。 したがって関数引数の個数に合わせてスタック・フレームの大きさを管理するのは、関数の呼出側の責任である。 たとえば Tiny C コンパイラでは、関数から戻ってきた直後に %esp の値を引数の大きさの分だけ減らさなければならなかった。

関数引数は、呼出し側のスタック・フレームの中ではなく、その上、つまり呼ばれた側の関数のスタック・フレームの一部となるように積む方法もありえる。

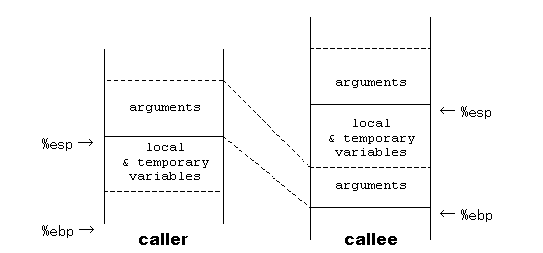
実際、Pascal の処理系では後者の方法をとる。 しかし後者の方法では、printf() のような可変長の引数をとる関数をコンパイルできない。 なぜなら呼ばれる側の関数のスタック・フレームの大きさは、引数の個数に依存するので、コンパイル時に引数の個数が不定であると、コンパイラがその関数のスタック・フレームの大きさを決められなくなってしまうからである。 このため C 言語では、前者の方法をとっている。

後者の方法の利点は、中から他の関数を呼ばない関数 (leaf 関数) の実装を高速化できる点である。 前者の方法では、leaf 関数を呼んだ場合も、呼出し終了後、常に呼出し側の関数が %esp の値を操作してしまう。 一方、後者の方法では、関数引数の個数に合わせてスタック・フレームの大きさを管理するのが呼ばれた側の関数なので、leaf 関数の場合は、スタック・フレームの管理を省略して高速化することができる。 スタック・フレームの管理のために %ebp, %esp を操作するのは、さらなる関数呼出しに備えるためであり、leaf 関数のようにそれ以上関数を呼び出さない場合は %ebp, %esp の値をそのままにして関数本体を実行することが可能である。

なお、以上の議論は x86 アーキテクチャの場合である。 対象となるプロセッサのアーキテクチャおよび calling convention によっては、ふたつの方法の利点・欠点は変化する。

課題 8

Copyright (C) 1999-2000 Shigeru Chiba